Способы штриховки куба

Диагностика проблем

При выводе трёхмерных тел встречается ряд типовых ошибок. Если что-то не работает, пройдитесь по следующему чеклисту:

• вы не забыли вызвать glBegin/glEnd до и после вызова glColor/glVertex?
• тело не выпадает из порта просмотра из-за матрицы GL_PROJECTION?
• тело не обрезается дальней и ближней плоскостями отсечения из-за матрицы GL_PROJECTION?
• в массиве индексов нумерация вершин начинается с нуля?
• включён тест глубины и режим отсечения задних граней?
• в массиве индексов вершины примитивов (треугольников и четырёхугольников) перечислены по часовой стрелке для внешнего наблюдателя?

Если всё нормально, то вы получите статичное изображение куба без возможности поменять положение камеры:

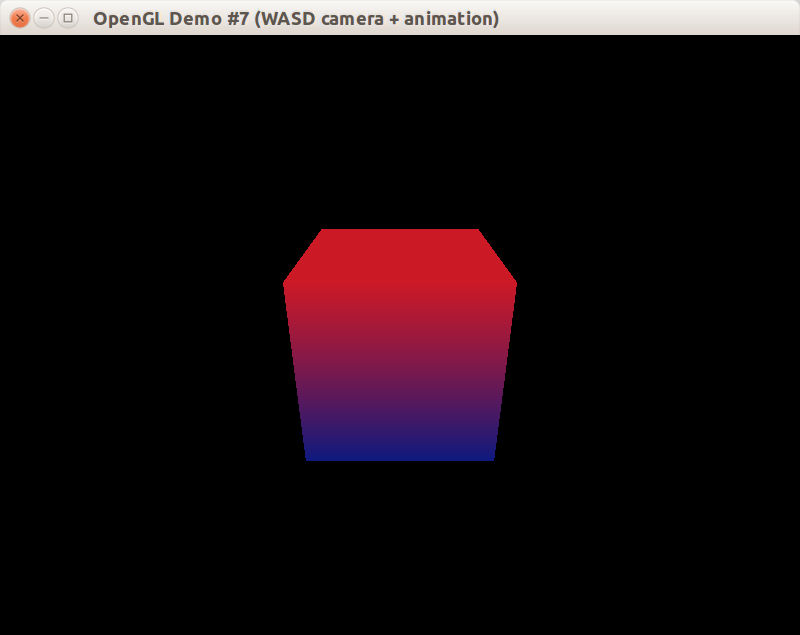
Чтобы придать сцене динамику, нам потребуется глубже изучить математические принципы трансформаций точек и векторов в трёхмерном пространстве. Приступим…

Преимущества кубов из бумаги и картона

Среди положительных моментов формирования фигуры из картона или бумаги выделяют:

• возможность быстрой сборки;
• отсутствие материальных затрат – бумага, клей и ножницы есть у каждого;
• возможное привлечение детей в процесс – представленным образом можно занять детей на длительное время;
• порча готового изделия не принесет моральных страданий, потому что можно всегда сделать новую форму.

Оригами из бумаги КУБИКИ ТРАНСФОРМЕРЫ

Оригами из бумаги КУБИКИ ТРАНСФОРМЕРЫ — движущаяся поделка антистресс и игрушка своими руками!

8.5 Общий Балл

Сделать кубик из картона или бумаги

Достоверность информации

8

Актуальность информации

9

Раскрытие темы

8.5

Доступность применения

7.5

Плюсы

• Поделки из бумаги — увлекательное и интересное занятие
• Развивает мелкую моторику и фантазию

Минусы

• Вам понадобится качественная бумага
• Необходимы определенные навыки

Как нарисовать куб карандашом объёмно

В основе любой формы лежат базовые геометрические фигуры. Самая часто встречающаяся это куб. Нарисовать геометрические фигуры в объёмном 3д виде не так просто как кажется, особенно если вы занимаетесь этим впервые. Обучение объёмному рисованию начинается с куба. Чтобы понять, как нарисовать куб карандашом объёмно, мы подобрали для вас несколько инструктажей.

Начнём с простого примера, который поможет новичкам. Для этого рисунка воспользуемся простым карандашом, линейкой и ластиком. Переходим к шагам:

В верхней части листа нужно нарисовать длинную линию. Разместите её в горизонтальном положении. Отступаем от края приблизительно один сантиметр. Добавляем вторую линию. Её нужно начертить под наклоном, чтобы получился острый угол.
Отталкиваясь от полученных линий нужно сделать треугольник, так как это показано в примере. Чертим вторую линию, с другой стороны, и соединяем на конце с первой полосой. С левой стороны чертим ещё одну полосу, но доводить её до конца не нужно.

Внутри полученного треугольника нужно изобразить ещё один, но меньше. Углы располагаются параллельно друг другу.
Выше полученных треугольников рисуем следующую линию, доводим её к правой стороне нижнего треугольника. Работу повторяем и, с другой стороны

Обратите внимание, что эти полосы пересекаются и образуют квадрат. Это верхушка куба.

1. Создадим грани фигуры. Добавляем вертикальные линии. Их нужно провести по бокам и в передней части от углов. Сзади грань не рисуем, её не будет видно.

Стираем все вспомогательные линии, помеченные пунктиром оставляем только нужную фигуру. Вот как нарисовать куб поэтапно, его можно раскрасить в любой цвет

Но обратите внимание, что его стороны не должны иметь равномерный окрас. Те, что расположены ближе к нам, имеют тёмный оттенок

Верхушка остаётся светлой.

Вертикальные линии и невидимые грани

Обратите внимание на снимок куба в самом начале статьи. На нем отчетливо видно, что линии, которые расположены вертикально, немного наклонены

Это, прежде всего, связано с тем, что объектив фотокамеры, с которой производился снимок, увидел перспективное сокращение линий.

И это правда, когда мы видим куб сбоку и сверху, кажется что вертикальные линии чуть-чуть сходятся в одну точку которая располагается снизу. Академический рисунок игнорирует передачу сокращения вертикальных линий, за исключением случаев сильного ракурса, а при начальном уровне обучения, куб рисуется с параллельными вертикальными линиями, строго перпендикулярными линии горизонта.

Как только нарисованы верхние линии, проверяем, насколько сократились боковые грани с обеих сторон. Ширину данных граней меряем только по горизонтали, ни в коем случае не под наклоном, и переходим к сравниванию, какая из них меньше высоты самого ближнего бедра куба, и обязательно без между собой. Как только закончите с проверкой ближних линий и вертикальных ребер можете приступать к зарисовке дальних уходящих линий.

Невидимые линии также обязательно следует рисовать. Перед тем, как будете рисовать самое дальнее вертикальное бедро, убедитесь, что их точки схода расположены правильно. Если они расходятся и это заметно, то необходимо еще раз все тщательно проверить и исправить рисунок, самое главное не испортить его. Если расхождение линий не такое большое, необходимо просто немного подкорректировать линии и нарисовать дальше бедро, которое будет располагаться вертикально.

Как только, вы закончили с построением, выделите ближние к себе линии. Если линия темная — будет казаться, что она ближе. Зная это, можно передать пространство и объем.

Построение куба:

Поставьте куб на ровную поверхность.
Определите свое положение относительно куба, лучше всего куб выглядит, когда видно три плоскости куба.
Определите линию горизонта, зафиксируйте её для себя, если линия горизонта попадает на плоскость бумаги, то обозначьте её на листе.
Сразу задайте основную грань куба, первую высоту можно обозначать свободно

Важно помнить, что куб по законам композиции должен находится ближе к верхней границе листа. Правильным считается, когда под кубом пространства остается больше, чем над ним.

• Обозначаем линии граней в виде линий перспективного сокращения.
• С помощью карандаша измеряем соотношения сторон относительно высоты куба, которую мы задали первично. На линиях перспективного сокращения отмечаем длину сторон куба.
• Любые измерения нужно осуществлять на вытянутой руке, держать карандаш строго горизонтально или вертикально, в зависимости от того, какие ребра куба нам нужно отрисовать.
• Обозначаем наши линии легким нажатием, чтобы в будущем линии возможно было легко стереть. Построение должно быть четким и чистым, избегайте лохматых линий. Все точки схождения граней должны быть чистыми и идеальными.

• После того, как вы убедились, что куб построен правильно, можете убрать лишние линии построения. Если вы строите куб первый раз, то можете оставить линии построения, чтобы в дальнейшем возвращаться к этому упражнению, когда будете изучать более сложные предметы.
• Во время штриховки придерживаемся главных правил — всегда набираем тон равномерно, в любой момент времени куб должен выглядеть завершенным. Можете заштриховать куб и фон вокруг куба, помните, что куб — гипсовый белый предмет, он не может быть намного темнее окружающего пространства.
• После того, как общий тон набран, можете усилить теневые места и самую близкую к вам гранью Не забываем принципы световой перспективы — чем ближе к нам предмет (в данном случае грань куба), тем она ярче, чем дальше — тем тусклее.
• В процессе штриховки избавляемся от четких контуров, обводка в академическом рисунке недопустима и является одной из главных ошибок.

Упражнение на построение куба является универсальным для понимания построения архитектуры и дизайна, поможет правильно изображать уже более сложные предметы.

Did you find apk for android? You can find new Free Android Games and apps.

Как нарисовать куб в перспективе со штриховкой

На примере следующей работе разберем основные принципы построения пошагово и просто. Перед началом необходимо знать лишь базовые квадратные формы, поэтому урок подойдет для детей 6-го класса. Рекомендуем набить руку в рисовании прямых линий без линейки, для этого просто потренируйтесь на листе проводить их без посторонней помощи. С таким навыком изображение получится намного быстрее.

Если вам слишком сложно воспринимать объем, перед собой поставьте что-либо кубической формы, это может быть колонка или коробка. Видя в живую силуэт, вам будет легче воплотить его на бумаге. 

Подготовьте карандаш мягкостью HB и приступаем к творчеству:

Куб состоит из шести квадратов, поэтому сначала мы изобразим их основные грани. Помните, что все они равны между собой. У основания обозначаем горизонтальный вспомогательный ориентир, находящийся под наклоном. От него и расходятся все остальные плоскости. Учитывайте, что левый луч расходится под большим углом.

Вырисовываем вертикальные полосы и соединяем их сверху. Прорисовываем продолжение всех направляющих, они будто стремятся сойтись где-то далеко.

Будем строить предмет насквозь, будто он прозрачный, поэтому покажем границы и внутри

Обратите внимание, что параллелепипед донышка чуть шире крышки. Обязательно проверяйте параллельность всех линий, они могут немного сходится, но ни в коем случае расходится

Стираем ластиком внутреннее построение, так как далее займемся тонировкой. Верхнюю плоскость оставляем не закрашенной. Левую вертикальную область наполняем лишь слегка. Самой темной частью будет лицевая. Направление штрихов должно быть параллельно граням. Фон оформляем диагональными движениями.

Повторно выделяем края. Закрашивая стол, придерживаемся горизонтального направления штриха. Тонально он темнее левой плоскости куба. Самое темное пространство — это тень, она будет падать справа. Чем ближе она к объекту, тем более она насыщенная и четкая.

Затемняем границы у освещенных граней, чтобы выделить их. Так, верхний левый угол должен быть самым насыщенным. Прорабатываем и уточняем рисунок, внимательно рассматривая натуру или фото.

У нас получился настоящий графический шедевр! Развивайтесь и изображайте другие фигуры, например, пирамиды или шары. Творческих успехов!

Объемные бумажные кубики без клея и ножниц

Задумывались ли вы о том, как сделать куб из бумаги и зачем это нужно? Допустим, как сделать кубик из картона своими силами, мы вам расскажем и даже покажем.

А какими полезными функциями вы наделите кубик оригами? Подскажем: вспомните свои детские кубики с буквами, из которых вы учились складывать первые слова, еще не умея писать.

А если бумажный кубик оклеить картинками из старых детских книжек, получится не менее интересный, чем в нашем далеком детстве, пазл-конструктор.

Вариантов игрового применения куба из цветной бумаги не счесть. И при этом не придется переживать, что дети поранят друг друга, кидая такую игрушку. Наши-то деревянные были потяжелее. Мы уже готовы показать, как сделать кубик из бумаги своими руками прямо сейчас. Готовы приступать?

Простой бумажный кубик

Объемный шестигранный куб 3Д складывают из квадратного листка бумаги без клея. И даже ножницы здесь не потребуются. Разве что отрезать лишний «хвостик» от листа А4, чтобы получить заготовку-квадрат. Зато пригодится навык надувания воздушных шариков, ведь мы сейчас научим вас тому, как сделать надувной кубик. Заинтригованы? Тогда начнем:

• Схема 1 — ваш наглядный ориентир. К нему следует прибегать каждый раз, когда алгоритм складывания кажется сложным. Возьмите бумажный квадрат и сложите его по диагоналям, затем пополам — все это просто разметка;
• Ориентируясь на диагонали-сгибы, сформируйте треугольник, подгибая внутрь боковые плоскости заготовки (см. схему). 4 гуляющих угла у основания треугольника нужно подогнуть к вершине по 2 с каждой стороны заготовки;
• Боковые противоположные уголки подогните к центру — у вас здесь есть вертикальная ось-ориентир. Повторите действие с другой стороны. Гуляющие уголки одного из конических выступов (на втором углы «закрыты») дважды подгибают, чтобы их можно было аккуратно заправить в срединные уголки-кармашки;
• Аналогично заправьте дважды сложенные уголки в кармашки с обратной стороны заготовки. Модель куба готова, осталось дать ей объем. Найдите открытый уголок и через него надуйте макет.

Куб из модулей: сборный кубик 6 цветов

Как сделать кубик из картона своими силами мы уже рассмотрели выше, а для этого модульного куба будет достаточно разноцветной бумаги 6-ти расцветок (или 3-х повторяющихся). Он и без картона получится достаточно плотным за счет алгоритма складывания модулей (каждого в отдельности и всех воедино).

Давайте начнем разбираться поэтапно. Сразу предупредим, что весь процесс будет разделен на 7 шагов — складывание модулей и сборка куба (можно на клей — будет прочнее).

Какое-то время будет потрачено, но результат вас однозначно порадует: кубики получатся яркими, разноцветными, не нуждающимися в дополнительных украшениях или росписи.

• Возьмите квадратный листок бумаги и сложите его так, чтобы получилось видимое разделение на 4 одинаковых прямоугольных плоскости (см. рис. 2). Загните малые уголки по диагональным углам стартового квадрата;
• Заверните «створки» листа подобно закрытию оконных ставней. Используя ориентиры-уголки (подогнутые ранее), загните внутрь незадействованные прежде углы, потом заправите их внутрь с обеих сторон. Получится параллелограмм;
• Переверните конструкцию вниз лицом, отогните уголки к себе так, чтобы получился маленький квадрат с треугольными ушками-отгибами. Сделайте еще 5 шт. таких модулей.

Соединяйте блоки в куб, вводя уголки модулей в срединные плоскости-кармашки соседних блоков. Проявите смекалку, в крайнем случае поможет схема. Как сделать оригами кубик из ярких модулей, вы освоили на практике. Попробуйте склеить куб из блоков на этапе сборки, чтобы он был еще прочнее и не рассыпался на модули в игре.

Можно, конечно, взять стандартную развертку куба, просто распечатать ее и склеить — готовые шаблоны всегда под рукой. А если типовая выкройка вас не устраивает и в игру нужен оригинальный счетный кубик, вы на раз-два сможете его сложить сами. Чего проще, когда знаешь, как сделать из бумаги еще и не такие премудрости.

Возможно, вас заинтересуют схемы складывания бумажной гадалки или лягушки, которая открывает рот.

Модульный кубик

Чтобы сделать модульный куб, необходимо взять 6 листов цветной бумаги. Они могут быть одинаковыми или разными по цвету. Желательно, чтобы каждый 2 листа были одинакового оттенка. Как сделать кубик из модулей:

1. Вырезать из бумаги 6 квадратов размером 15 на 15 см.
2. Первый из них согнуть пополам для создания складок, затем снова развернуть.
3. Ориентируясь на центральную складку, сложить две стороны квадрата к середине.
4. Перевернуть листик и каждый его угол сложить по направлению к центральной части.
5. По итогу должна получиться трапеция. Складывать потребуется только противоположные углы.
6. Загнуть углы трапеции к середине с другой стороны.
7. Опустить все углы.
8. Все те же действия повторить с другими квадратами, которые будут использоваться для создания объемного куба.
9. Теперь можно приступать к сборке модулей. Для этого нужно взять две детали одинакового цвета. Угол первой их них потребуется вставить в тело второй.
10. Вставить второй модуль в другую сторону. Одно открытие на получившихся квадратах вмещает два треугольника (язычка модуля).
11. Продолжать складывать модули, пока не образуется цельное изделие.

Модульный кубик готов.

Готовый модульный кубик.

Работы в трехмерном исполнении

А вот такие работы, исполненные в трехмерном пространстве, можно отыскать в интернете. Они просто поражают воображение глубиной и качеством. Компьютерная графика в наше время может все. Ведь рисовать можно не только на бумаге, но и, изучив специальные программы 3D моделирования, на персональном компьютере.

Ниже на рисунках вы увидите завораживающие модели объемного мира трехмерного изображения.

Изображения в трехмерном пространстве, благодаря воссозданию объемности, завораживают душу человека и словно тянут ее за собой, не разрешая ни на секунду оторваться от любования прекрасной картиной.

Новогодний светящийся снеговик своими руками, пошагово с фото

Светящегося снеговика можно сделать не только из дюралайта, но и другим не менее интересным способом, используя одноразовые стаканчики:

Купите 300 одноразовых пластиковых стаканчиков белого цвета:

Возьмите 25 стаканчиков и скрепите их по кругу с помощью термопистолета или же степлера:

В шахматном порядке сверху первого ряда выложите стаканчики в 7 рядов, скрепляя их не только снизу и сбоку, но и сверху между собой, чтобы конструкция была прочной:

Сделайте еще одну такую конструкцию, внутрь каждой поместите светодиодные гирлянды, а затем скрепите их между собой степлером. Украсьте снеговика так, чтобы у него были пуговицы и нос. Можно использовать любые канцелярские принадлежности для этого и не только:

Волшебство праздника мы создаем себе сами, поэтому не ждите от кого-то приятных сюрпризов, создавайте их сами с удовольствием! Пусть наши советы и рекомендации выручают вас в повседневной жизни, помогая сделать праздник незабываемым!

Матрица поворота

Матрица поворота воздействует и на точку, и на вектор, при этом удалённость точки от начала координат и длина вектора не меняются. Существует Теорема Эйлера, согласно которой любой поворот в трёхмерном пространстве вокруг произвольной оси можно представить как последовательность трёх поворотов вокруг трёх базовых осей системы координат в определённом порядке и на определённые углы:

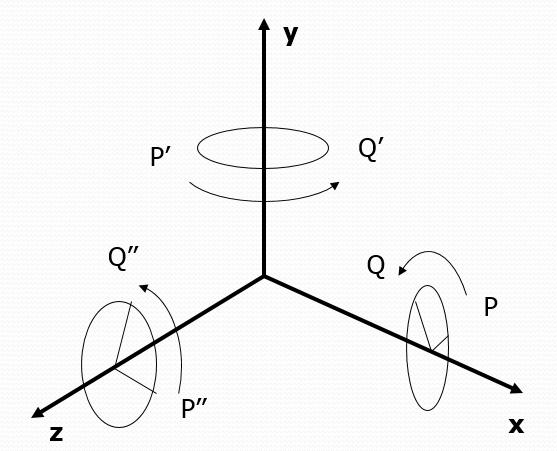
Перечислим три матрицы поворота на угол “a” вокруг трёх осей системы координат (посмотреть, что получается при перемножении, вы можете самостоятельно):

В GLM есть функция , умножающая переданную матрицу на матрицу поворота вокруг переданного произвольного вектора оси на переданный угол. Как уже было сказано ранее, следует настроить GLM так, чтобы углы выдавались в радианах — иначе вы будете получать предупреждения об использовании устаревшего API. Проверьте, что в перед включением GLM объявлен макрос GLM_FORCE_RADIANS:

Матрицы поворота сложнее масштабирования или перемещения, но применить их для анимации проще: нужно всего лишь задать скорость поворота такой, чтобы за время анимации куб повернулся целое число раз:

Вот так это будет выглядеть к концу урока:

Шаг 4 — Проверка пропорций

Для того, чтобы проверить пропорции, закройте один глаз, возьмите карандаш и на вытянутой руке сопоставьте его кончик с верхом переднего ребра куба. Большой палец передвиньте в то место, где ребро заканчивается.

Высота ребра найдена. Теперь, не переставляя палец, наклоните кисть руки на 90 градусов и уже по горизонтали сопоставьте величину одного ребра с другим. Таким образом вы можете проверять и другие величины.

С опытом художники измеряют пропорции «на глаз», это значит, что они обходятся без метода визирования. Их глаз настолько натренирован, что видит размеры без измерений.

Итак, линейное построение подошло к концу, а значит, мы переходим к воздушной перспективе или, проще говоря, к штрихованию.

Как собрать кубик Рубика — пошаговая схема для начинающих в картинках

Нужно собрать края одной стороны. Для начала выберите цвет, который будет первым. Пусть это будет желтый. Итак, начнем! Поверните куб желтым цветом кверху, таким образом снизу останется белый, практически во всех существующих моделях представлена эта разметка.

Пользуясь нашим советом, помните, что нужно сделать по порядку. Второй цвет ребра должен соответствовать центральной частице, которая ближе всего. Потренируйтесь и у вас получится. Главное — не останавливайтесь, попробуйте во всем разобраться и продвигайтесь с уверенностью дальше. Вам в помощь придет терпение и еще раз терпение, не сдавайтесь. Соберите крест по схеме, но не забывайте, что это нужно будет сделать 4 раза — для каждой стороны. Куб должен быть у вас в руках, переворачивайте его, сверху должен быть желтый центровой элемент, или тот, цвет, который вы подобрали, внизу — белый

Посмотрите, есть ли желтый внизу, и обратите внимание на оба цвета ребра.В том случае, если вами был найден желтый квадратик, крутите куб, пока ребро не займет свое место сверху. Продолжайте следовать инструкции, как собрать кубик Рубик по схеме для начинающих по фото и выполните одно из действий: центр — внизу, впереди, ребро — в промежуточном слое и повторите шаг номер 1

Край будет стоять в положении, описанном ранее, с помощью схемы он встанет на свое место. Так нужно сделать для каждого из желтых кубов, в итоге вы получаете крест.

Основание куба

При рисовании основания куба очень важно определить углы наклона основных видимых граней, относительно основания. Это можно сделать очень простым способом: необходимо поднести карандаш на расстоянии вытянутой руки в строго горизонтальном положении к нижнему ближнему углу и запомнить углы, но не пытайтесь просто переносить углы на холст с помощью карандаша, это неправильно

Пытайтесь запомнить их и повторять. Только так будет «набиваться» рука и глазомер.

Далее необходимо учесть, что если грань куба больше развернута к вам, то угол меньше. Так можно определить какая грань меньше развернута, а какая — больше.

Можете нарисовать нижние грани, но до того, как перейти к началу рисования верхних, необходимо подумать над основным законом перспективы, который гласит, что любые параллельные линии, уходящие от зрителя, сокращаются в одну точку — точку схода.

У нашего куба имеется четыре ребра, которые смотрят направо и столько же ребер налево. Все четыре линии ребер, которые уходят влево, при их продолжении, сокращаются в одной точке схода слева, а все линии, которые уходят вправо — сходятся справа.

Но как правильно определить где все эти точки будут сходиться? Куб расположен на горизонтальной плоскости, а она параллельна поверхности земли как пол, стул и стол. И если наши линии удаляется от какого-либо предмета, то точка схода должна лежать именно на линии горизонта.

Но где же располагается линия горизонта? Всё просто: она всегда расположена на уровне глаз человека. Куда бы вы не смотрели — линия горизонта будет ровно на уровне ваших глаз. Проведите небольшое исследование: посмотрите в окно и представьте, где сходится земля с небом. Ответ будет очевиден. Даже если мы присядем, то и линия горизонта опустится.

Линию горизонта и точки схода рисуют тонкими линиями на листе до того, как нарисовать верхние грани.

Главные принципы и особенности строения трехмерных проекций n-мерных гиперкубов

Прежде чем приступить к построению (черчению) трехмерных проекций n-мерных гиперкубов,
оговорим некоторые закономерности, особенности, главные принципы строения этих геометрических фигур.

Предлагаю вашему вниманию главные геометрические свойства и особенности трехмерных проекций
всех n-мерных гиперкубов (3ПГК-n) и разработанные принципы, методы, правила создания,
построения и черчения трехмерных проекций n-мерных гиперкубов (3ПГК-n).

1. Во всех n-мерных гиперкубах, а также и в их трехмерных проекциях, в каждой вершине сходятся по n ребер.
То есть: в каждой из 16-ти вершин 3ПГК-4 сходятся по 4 ребра, в каждой из 32-х вершин 3ПГК-5
сходятся по 5 ребер, в каждой из 64-х вершин 3ПГК-6 сходятся по 6 ребер, и т.д.

2. Во всех трехмерных проекциях n-мерных гиперкубов (см. рис. 1.1)
в первом «ярусе» (то есть между параллельными плоскостями Р_I и Р_II)
и в последнем «ярусе» (между параллельными плоскостями Р_n и Р_n+I)
находятся по n ребер, сходящихся в верхней вершине, расположенной в плоскости РI, и в нижней вершине,
расположенной в плоскости Рn+I.

Эти n ребер можно (и нужно) представить как боковые ребра правильной n-угольной пирамиды.
Эти пирамиды назовем «исходными» пирамидами.

Вот это и есть очень важная (главная) для построения и черчения трехмерных проекций
n-мерных гиперкубов особенность:

а) в любой 3ПГК-n в первом и в последнем «ярусах» заключена часть тела 3ПГК-n
в виде правильной n-угольной пирамиды;

б) по построенной «исходной» правильной n-угольной пирамиде в любом
ракурсе, в любой проекции можно построить (начертить) и 3ПГК-n в выбранных ракурсах и проекциях.

3. Любое ребро n-мерного гиперкуба (ГК-n), а также его трехмерной проекции (3ПГК-n)
геометрически равно по длине и параллельно одному из n боковых ребер т.н. «исходной»
правильной n-угольной пирамиды, расположенной в первом или последнем «ярусе» ГК-n или 3ПГК-n.

4. Отрезок прямой в теле 3ПГК-n, соединяющий вершины, расположенные в параллельных плоскостях
Р_I и Р_n+I, т.е. вершины верхней и нижней «исходных» правильных
n-угольных пирамид (см. рис. 1.1), перпендикулярен этим плоскостям Р_I и Р_n+I
и является главной осью симметрии 3ПГК-n.

5. В n-мерных гиперкубах, где n – четное число, а также в их трехмерных проекциях
(т.е. в 3ПГК-4, 3ПГК-6, 3ПГК-8, 3ПГК-10, и т.д.), обязательно существуют
геометрически обусловленные совмещенные (сдвоенные) вершины, расположенные в точках
пересечения визуально проведенной главной оси симметрии 3ПГК-n с визуально обозначенными на
рис. 1.1 параллельными плоскостями: Р_III — в 3ПГК-4; Р_III и
Р_V — в 3ПГК-6; Р_III , Р_V и Р_VII — в 3ПГК-8, и т.д.

В этих геометрически обусловленных совмещенных (сдвоенных) вершинах 3ПГК-n соответственно
сходятся по 2n ребер, вот почему я написала фразу: «… в большинстве случаев избежать
совмещения вершин и ребер практически невозможно».

6. При изображении 3ПГК-n (черчении или фотографировании их моделей) в разных ракурсах возможны
визуальные совмещения любых вершин, а также визуальные совмещения ребер, граней и даже кубов.